備註：我對機率這門學問明顯並非通熟。這份筆記的內容都只是我的片面見解，若有思考錯誤之處還請指正～大感恩🙏

機率 (Probability) 是面對未知的現象時，根據現有的資訊以數學方式建立起來的模型。為了確定建立起來的模型跟『想像中的現實』是否一致，通常會以蒙地卡羅模擬 (Monte Carlo Simulation) 作為輔助，為自己建立出來的模型提供實驗佐證。

有趣的是，這些『想像中的現實』與『人的直覺』偶有相左之處。這時候就會形成有趣的機率悖論 (probability paradox)，透過實驗的方式，能讓我們更能夠澄清或了解這樣的現象。今天我們將舉一個比較平易近人的例子：Monte Hall Problem，中文譯作蒙特霍問題、或是三門問題。這個問題在維基百科中有超詳盡的來龍去脈：https://en.wikipedia.org/wiki/Monty_Hall_problem。

在當年爆紅的美國電視節目中，問題的設定是這樣子的：有三扇門，兩扇門後面各自有隻山羊、另一扇門後面有輛車。在活動開始之前，主持人隨機選一扇門並且將車輛放在該門後面。活動進行時，活動來賓率先選擇一扇門。由於剩下的兩扇門，其中一扇後方必定有山羊，主持人將打開該門，並且問來賓『是否要更換選擇的門？』

此時，來賓可以有諸多選擇，他可以依照任何理由、制定任何策略來決定是否更換選擇的門。這個問題最酷的地方在於，此時的來賓若『打從一開始就決定要換門』，成功獲得汽車的機率竟然有 2/3 這麼多。現在就讓我們實際模擬這個流程，看看到底是不是 2/3。

import random
from matplotlib import pyplot as plt
import numpy as np
plt.style.use("seaborn-v0_8") # beautiful!

# 定義三種策略：總是不換；總是換門；總是丟個銅板決定要不要換。
from enum import Enum
Strategy = Enum("Strategy", ["ALWAYS_KEEP", "ALWAYS_SWAP", "RANDOM_CHOICE"])

這邊定義一次模擬：根據所選的策略，會得到汽車或山羊。

def monty_hall(strategy):
    # 先定義門後面有啥。
    behind_doors = ["CAR", "GOAT", "GOAT"]
    
    # 隨機選一扇門，並拿到門後面的東西。
    grab_one = random.choice(behind_doors)
    
    # 主持人把另一扇門打開。
    behind_doors.pop(behind_doors.index(grab_one))
    behind_doors.pop(behind_doors.index("GOAT"))
    
    # 這時候根據你的策略決定要不要換。    
    if strategy == Strategy.ALWAYS_KEEP:
        pass
    
    elif strategy == Strategy.ALWAYS_SWAP:
        grab_one, behind_doors[0] = behind_doors[0], grab_one
        
    elif strategy == Strategy.RANDOM_CHOICE:
        if random.choice(["SWAP", "NOSWAP"]) == "SWAP":
            grab_one, behind_doors[0] = behind_doors[0], grab_one
    
    # 回傳最後拿到的。
    return grab_one

接下來就可以跑很多次模擬並且製圖啦～

# 我們將進行實驗 10000 次。
N = 10000

strategy = Strategy.RANDOM_CHOICE # 修改這個
results = [monty_hall(strategy) for _ in range(N)]

# 把結果繪製出來
plt.figure(figsize=(8, 1))
plt.barh(*np.unique(results, return_counts=True))
ax = plt.gca()
ax.bar_label(ax.containers[0], label_type='edge')
ax.set_title(strategy)
plt.show()

實驗結果

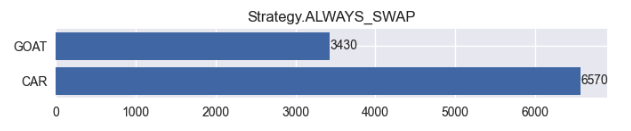
如果我們選擇的是『永遠要換』那麼實驗中拿到汽車的次數，的確佔了大約三分之二。

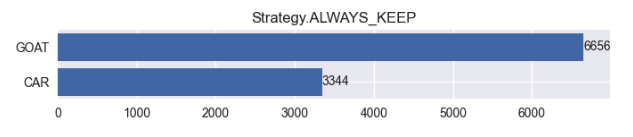
如果我們選擇的是『永遠不換』那麼實驗中拿到的汽車次數，的確只佔了三分之一。

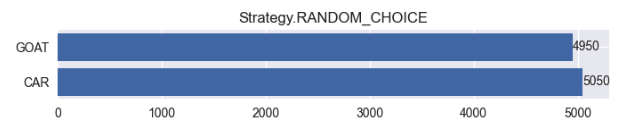
如果我們選擇的是『隨機更換』那麼實驗中拿到的汽車次數，大約只佔的二分之一。